机器学习总结（五）优化算法之梯度下降法

在机器学习中，优化损失函数的算法对于优化损失函数非常重要，它决定了损失函数的收敛速度，是否容易收敛甚至能不能收敛，是否收敛在全局最小处。

本文主要总结一种常见的优化 损失函数的算法，即梯度下降法：

梯度下降法是求解无约束最优化问题的一种最常用，最经典的算法，有实现简单的优点。它是一种迭代算法，每一步需要求解的目标函数的梯度向量。其不仅常用于机器学习算法 ，而且也是深度学习常用的优化算法。本次主要总结梯度下降法的原理，以及其变化 形式，各种变化形式的特点。

原理：梯度下降算法背后的原理：目标函数关于参数的梯度将是目标函数上升最快的方向。对于最小化优化问题，只需要将参数沿着梯度相反的方向前进一个步长，就可以实现目标函数的下降。这个步长又称为学习速率。参数更新公式如下：

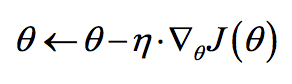
其中是参数的梯度。根据计算目标函数采用数据量的不同，梯度下降算法又可以分为批量梯度下降算法（Batch Gradient Descent），随机梯度下降算法（Stochastic GradientDescent）和小批量梯度下降算法（Mini-batch Gradient Descent）。

批量梯度下降算法：是在整个数据集上计算J（θ）后才进行梯度下降，数据集大的话容易造成内存不足，其优化一般比较慢。（与数据集的大小有关，一般数据集大的话，不采用）。

随机梯度下降算法：是在一个样本上计算J（θ）后就进行梯度下降，是批量梯度下降算法的一个极端。其迭代收敛速度一般会快些，但是由于样本的随机性强，每一步迭代并不一定朝梯度下降的方向进行，虽然整体会朝梯度下降方向进行，但无法达到全局最小值。此外，其丢失了向量化计算带来的计算加速。

小批量梯度下降算法：小批量梯度下降算法是批量梯度下降算法和随机梯度下降算法的折中，选取训练集中一个小批量样本计算，这样可以保证训练过程更稳定，而且采用批量训练方法也可以利用向量化计算的优势。这是目前深度学习中最常用的梯度下降算法。

动量梯度下降算法：

动量梯度下降算法是BorisPolyak在1964年提出的，其基于这样一个物理事实：将一个小球从山顶滚下，其初始速率很慢，但在加速度作用下速率很快增加，并最终由于阻力的存在达到一个稳定速率。对于动量梯度下降算法，其更新方程如下：

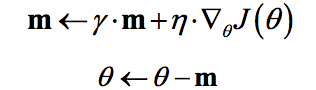
可以看到，参数更新时不仅考虑当前梯度值，而且加上了一个积累项（动量），但多了一个超参，一般取接近1的值如0.9。相比原始梯度下降算法，动量梯度下降算法有助于减少训练的震荡过程（变化对梯度减少的影响减小），但是可以加速收敛(m值还是会比较大)。

RMSprop优化算法

RMSprop（root mean square prop）算法的目的，主要是解决学习速率过快衰减的问题。其实思路很简单，类似Momentum思想，引入一个超参数，在积累梯度平方项进行衰减：

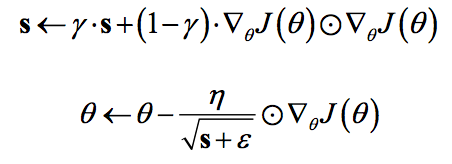
其中ε=10?8。该算法可以认为仅仅对距离时间较近的梯度进行积累，其实这样就是一个指数衰减的均值项，减少了出现的爆炸情况，因此有助于避免学习速率很快下降的问题。

 Adam （Adaptive Moment Estimation）优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法。算法中通常beta_1=0.9,beta_2=0.999

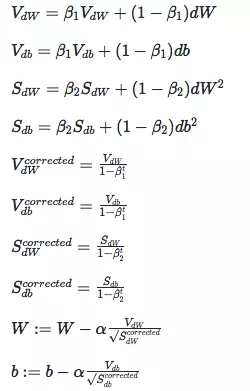
β1：常用缺省值为0.9，dwdw的加权平均；β2：推荐使用0.999，dw2dw2的加权平均值；ε：推荐使用10?810?8。

该算法结合了动量梯度下降法和RMSprop优化算法于一体，经常采用这种优化算法。